The shift from 32-bit to 1-bit representations in Large Language Models significantly enhances computational efficiency and scalability, while introducing challenges in information loss and model accuracy. Advanced techniques are employed to mitigate these issues, striking a crucial balance in the development of efficient machine learning models.

The move from 32-bit to 1-bit representations in Large Language Models (LLMs) stands as a pivotal advancement in machine learning, significantly enhancing computational efficiency and scalability. Let's look at the complexities behind this shift, focusing on the balance between computational savings and the potential for information loss and reduced accuracy.

Traditionally, Large Language Models (LLMs) use 32-bit floating-point numbers to represent word vectors, which allows for a detailed and nuanced representation of linguistic features. A 32-bit floating-point representation can capture a wide range of values with a significant degree of precision. For example, a word vector for "king" might be represented as [-0.856, 0.670, ..., -0.234], with each component of the vector being a 32-bit floating-point number. This precision enables the model to distinguish between subtle differences in meaning and context, capturing the complexities of language.

However, this precision comes at a cost. Each 32-bit floating-point number requires 32 bits of memory, so storing large numbers of these vectors—as is common in LLMs—can consume substantial amounts of memory and computational resources. The processing of these high-precision vectors also demands more computational power, impacting the efficiency and scalability of the models.

When we reduce these representations from 32-bit to 1-bit, each component of the word vector is compressed to a binary format, either 0 or 1. This process drastically reduces the memory footprint. For instance, the same vector for "king" might be simplified to a binary sequence like [1, 0, ..., 1], with each bit representing a drastically simplified version of the original vector components.

For a more concrete example, let's consider an LLM with a vocabulary of 10,000 words, each represented by a 300-dimensional vector. In a 32-bit setup, storing this vocabulary requires 96,000,000 bits (10,000 words * 300 dimensions * 32 bits). By quantizing to 1-bit representations, we reduce the storage requirement to 3,000,000 bits—a 32-fold reduction.

However, this simplification comes with trade-offs. The 1-bit representation significantly reduces the ability to capture the nuanced differences between words and linguistic features, potentially impacting the model's performance. The challenge then becomes how to effectively compress the data into 1-bit representations while minimizing the loss of information and preserving as much of the model's accuracy and capability as possible.

Advanced techniques like stochastic quantization, the Straight-Through Estimator (STE), and error feedback mechanisms are employed to address these challenges, aiming to maintain the integrity and performance of LLMs despite the reduced bit representation.

Stochastic quantization probabilistically quantizes weights, maintaining the original weight distribution more accurately. ¹

The Straight-Through Estimator (STE) is crucial for training quantized models, facilitating the backpropagation process to 'bypass' the non-differentiable quantization step. ²

Additionally, error feedback mechanisms play a vital role. If a weight is quantized inaccurately, the quantization error is used in subsequent training iterations to correct the model, gradually reducing quantization-induced inaccuracies.³

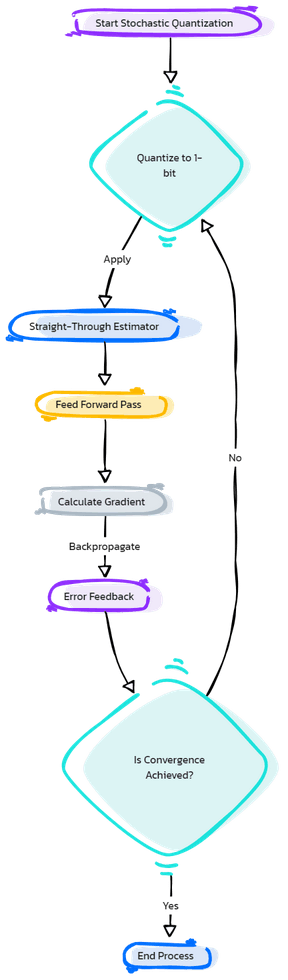
Figure: Flowchart depicting the process of stochastic quantization, application of the Straight-Through Estimator, and error feedback mechanisms in the context of 1-bit quantization.

So, if you are a .NET developer, using ML.NET, how do you implement these techniques?

Unfortunately, ML.NET does not have the capability to implement them directly, however, one can use a bridge to Python to access these capabilities.

For our example, let's assume that we have a Python script called quantize_model.py and a function in that script called perform_quantization.

There are 2 ways we can call Python libraries from ML.NET or C#:

1. Run Python scripts using the System.Diagnostics.Process class

   Make sure you have a Python environment set up, accessible from your system’s PATH with necessary libraries (e.g., NumPy, TensorFlow, or PyTorch for deep learning tasks) and of course our script named quantize_model.py that performs the quantization process.

   Here’s a basic outline for calling a Python script:

    using System;
    using System.Diagnostics;
   
    public class PythonIntegrationExample
    {
        public static void CallPythonQuantization()
        {
            // Define the path to the Python interpreter executable
            // This path might need to be adjusted based on your Python installation
            string pythonExecutable = "python";
   
            // Define the path to your Python script that performs the quantization
            string scriptPath = @"path\to\your\quantize_model.py";
   
            // Define any arguments your Python script needs
            string args = $"{scriptPath} arg1 arg2";
   
            // Set up the process start information
            ProcessStartInfo start = new ProcessStartInfo
            {
                FileName = pythonExecutable,
                Arguments = args,
                UseShellExecute = false,
                RedirectStandardOutput = true,
                RedirectStandardError = true,
                CreateNoWindow = true
            };
   
            // Run the process and capture the output
            using(var process = Process.Start(start)) 
            {
                using(var reader = process.StandardOutput) 
                {
                    string result = reader.ReadToEnd();
                    Console.Write(result);
                }
            }
        }
    }
   

2. Use the Python.NET package

   Install Python.NET via NuGet Package Manager to allow for more direct interactions with Python libraries from C# code. This method enables invoking Python scripts and functions as if they were native C# methods, offering a seamless integration between the two environments.

    using Python.Runtime;
   
    public class PythonNetExample
    {
        public static void CallPythonQuantization()
        {
            // Initialize the Python engine
            PythonEngine.Initialize();
   
            // Create a new Python scope
            using (Py.GIL()) // Acquire the Python Global Interpreter Lock (GIL)
            {
                try
                {
                    // Import your Python script as a module
                    dynamic quantizeModel = Py.Import("quantize_model");
   
                    // Assume your Python script has a function named 'perform_quantization'
                    // that takes no arguments and performs the quantization process
                    // Call this function
                    quantizeModel.perform_quantization();
                }
                catch (PythonException e)
                {
                    Console.WriteLine($"An error occurred: {e.Message}");
                }
            }
   
            // Shutdown the Python engine
            PythonEngine.Shutdown();
        }
    }
   

Potential Limitations and Challenges of Adopting 1-bit Representations:

While 1-bit representations offer significant benefits in terms of memory and computational efficiency, there are potential limitations and challenges to consider:

• Information Loss: The most significant challenge is the potential loss of information. Quantizing from 32-bit to 1-bit representations inherently reduces the granularity with which data can be represented, which could affect the model's ability to capture complex patterns.

• Model Accuracy: Although techniques like stochastic quantization, STE, and error feedback can mitigate accuracy loss, there's typically a trade-off between model size and accuracy. It's crucial to evaluate how these quantization techniques impact the specific tasks your model is designed for.

• Implementation Complexity: Integrating advanced quantization techniques, especially within environments like ML.NET which may not natively support them, adds complexity to the development process. It requires a solid understanding of both machine learning principles and software engineering practices.

Figure: The memory requirements and computational efficiency of 32-bit vs. 1-bit representations, highlighting the trade-offs and benefits.

In conclusion, the evolution from 32-bit to 1-bit representations in large language models marks a significant leap towards computational efficiency and model scalability.

By embracing advanced quantization techniques such as stochastic quantization, the Straight-Through Estimator, and error feedback mechanisms, we can navigate the challenges posed by information loss, ensuring minimal impact on model accuracy.

1. Stochastic quantization is a technique used in the quantization of model weights that introduces randomness in the process of converting continuous weights into discrete values. Unlike deterministic methods, which might always round a number to its nearest discrete counterpart, stochastic quantization probabilistically rounds numbers based on their value, allowing for a more accurate representation of the original weight distribution over time. This randomness helps in preserving the statistical properties of the original weights, thus mitigating the loss of information typically associated with quantization.

2. The Straight-Through Estimator (STE) is a method used to enable the training of quantized models, particularly addressing the challenge posed by the non-differentiable nature of the quantization function. During the forward pass, STE quantizes the weights for computation, but during the backward pass, it 'ignores' the quantization step, allowing gradients to pass through as if the operation were differentiable. This approach allows the model to adjust its weights through standard backpropagation, despite the quantization, facilitating the continued learning and refinement of the model.

3. Error feedback mechanisms are employed to address the inaccuracies introduced by quantization. When a weight is quantized, the difference between the original weight and its quantized value (the quantization error) is not discarded. Instead, this error is fed back into the model during subsequent training iterations. By incorporating the quantization error into future updates, the model gradually compensates for the inaccuracies introduced by quantization, leading to more precise weight adjustments and improved model performance over time.